Casually discussing code over coffee, a colleague introduced me to an intriguing geometry-infused LeetCode challenge. As I dedicated time to tackling the challenge, I crafted a straightforward probabilistic solution that successfully passed all the tests. However, the real excitement arose when my coworker shared an alternative approach that I couldn’t wait to showcase right here.
The problem
The problem is 1453. Maximum Number of Darts Inside of a Circular Dartboard. In simple terms, we are presented with a collection of points on a two-dimensional plane, along with a specified radius R. Our objective is to determine a circle with the radius R that encompasses the maximum number of points possible. The constraints are the following:
- At most 100 points.
- The coordinates are integers in the interval [-10^4, 10^4].
- The radius is at most 5000.
Note: For the sake of brevity we denote by C(R, x) a circle of the radius R around point x.
The straightforward “probabilistic” solution
As always, we begin by analyzing the constraints. We are dealing with, at most, 100 points, which suggests that an O(n^3) solution should be feasible. Now, a seemingly trivial yet crucial observation comes into play: the distance is symmetric. In other words, if point A lies within a circle C(R, X), then point X lies within the circle C(R, A). Consequently, when two points, A and B, reside within the circle C(R, X), X belongs to the intersection of circles C(R, A) and C(R, B).
These observations lead to the following probabilistic algorithm:
- Examine all pairs of points (A, B) within the dataset.
- For each pair, randomly sample point set X from the intersection of C(R, A) and C(R, B).
- Assess how many data points are located inside the circles C(R, x), where x belongs to X.
The primary advantage of the algorithm is its simplicity: I was able to come up with the idea and the draft implementation for about 30 minutes. However, a key drawback is that successful test passage necessitates parameter tuning. And naturally, the “probabilistic” aspect may not be well-received by a number of engineers(including myself).
Below is the very first working implementation in C#:
public class Solution
{
public int[][] points;
public int rSquare;
public int r;
double epsilon = 0.05;
public Random random = new Random();
public int NumPoints(int[][] darts, int r)
{
this.points = darts;
this.r = r;
rSquare = r * r;
var n = points.Length;
var result = 0;
for(int i = 0; i < n; ++i)
{
for(int j = i; j < n; ++j)
{
var intersection = GetIntersectionPoints(i, j);
foreach(var (x, y) in intersection)
{
var temp = 0;
foreach(var point in points)
{
if(IsInCircle(x, y, point[0], point[1]))
{
++temp;
}
}
result = Math.Max(result, temp);
}
}
}
return result;
}
public List<(double, double)> GetIntersectionPoints(int i, int j)
{
var result = new List<(double, double)>();
if(IsInCircle (points[i][0], points[i][1], points[j][0], points[j][1]))
{
var midX = (points[i][0] + points[j][0])/2.0;
var midY = (points[i][1] + points[j][1])/2.0;
result.Add((midX, midY));
for(int counter = 0; counter < 1500; ++counter)
{
var x = GetRandom(midX - r - epsilon, midX + r + epsilon);
var y = GetRandom(midY - r - epsilon, midY + r + epsilon);
if( IsInCircle(x, y, points[i][0], points[i][1]) &&
IsInCircle(x, y, points[j][0], points[j][1]))
{
result.Add((x,y));
}
}
}
return result;
}
public double GetRandom(double min, double max)
{
return random.NextDouble() * (max - min) + min;
}
public bool IsInCircle(double x1, double y1, double x2, double y2)
{
return Distance(x1, y1, x2, y2) <= r + epsilon;
}
public double Distance(double x1, double y1, double x2, double y2)
{
return Math.Sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
}
}And this approach is somewhat functional:
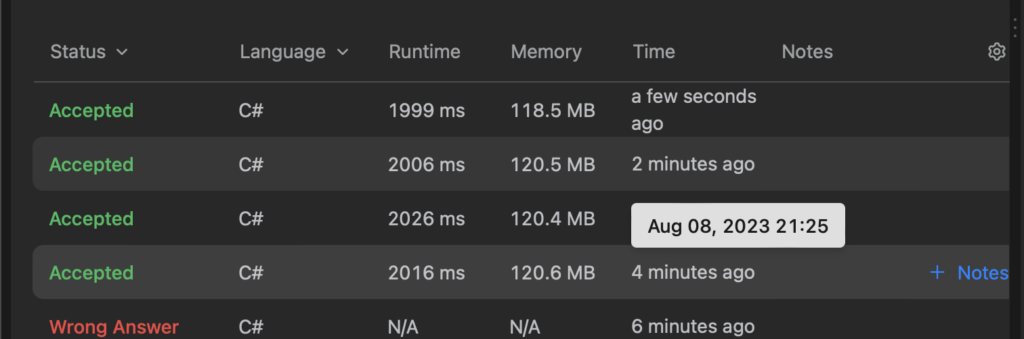
However, I found myself dissatisfied with the solution. Clearly, there are optimizations that could be implemented to enhance it, such as limiting the number of candidates we evaluate by precomputing distances between points in the data set. Or something like this where we sample points a bit differently:
public class Solution
{
public int[][] points;
public int r;
double epsilon = 0.01;
public Random random = new Random();
public int NumPoints(int[][] darts, int r)
{
this.points = darts;
this.r = r;
var n = points.Length;
var result = 0;
for(int i = 0; i < n; ++i)
{
for(int j = i; j < n; ++j)
{
foreach(var (x, y) in GetIntersectionPoints(i, j))
{
var temp = 0;
foreach(var point in points)
{
if(IsInCircle(x, y, point[0], point[1]))
{
++temp;
}
}
result = Math.Max(result, temp);
}
}
}
return result;
}
public List<(double, double)> GetIntersectionPoints(int i, int j)
{
var result = new List<(double, double)>();
if(Distance(points[i][0], points[i][1], points[j][0], points[j][1]) <= 2*r + epsilon)
{
for(int counter = 0; counter < 200; ++counter)
{
double angle = 2.0 * Math.PI * random.NextDouble();
var x = points[i][0] + r * Math.Cos(angle);
var y = points[i][1] + r * Math.Sin(angle);
if(IsInCircle(x, y, points[j][0], points[j][1]))
{
result.Add((x,y));
}
}
}
return result;
}
public bool IsInCircle(double x1, double y1, double x2, double y2)
{
return Distance(x1, y1, x2, y2) <= r + epsilon;
}
public double Distance(double x1, double y1, double x2, double y2)
{
return Math.Sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
}
}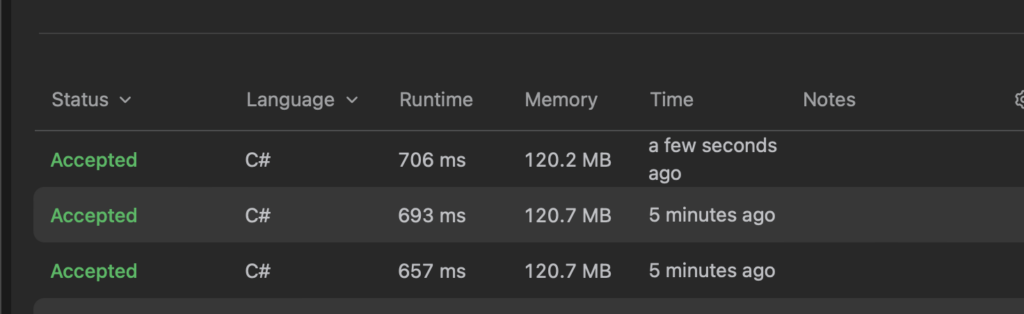
Overall it is about 3 times faster, yet it still seems like I may have been overlooking the fundamental idea behind the problem…
The colleague’s solution
Upon presenting this solution to my colleague, his surprise was evident. As someone with a mathematical background, I had overlooked a subtle detail that appeared intuitive to him, given his impressive computer science experience.
So the idea is as follows:
Consider the set of circles that yield the maximum value we are seeking in the problem. Within this set, there exists a circle that passes through at least two points in the dataset.
Of course this statement requires a rigorous proof, but we omit it here.
How do we use this statement? Well, the set of center’s of circles which contain two given points A, B is the line orthogonal to (A, B) passing through the mid point. Since the radius R is fixed there are only two such circles! Which lead to the following algorithms:
- Examine all pairs of points (A, B) within the dataset.
- For each pair, find two points X, Y such that the circles C(R, X) and C(R, Y) pass through both A and B.
- Assess how many data points are located inside the circles C(R, X) and C(R, Y).
The code kindly provided by the colleague:
public class Solution
{
public int NumPoints(int[][] darts, int r)
{
if (darts.Length < 2) {
return darts.Length;
}
return Solve(darts, r);
}
public int Solve(int[][] darts, int r) {
var res = 1;
for (var i = 0; i < darts.Length; ++i) {
for (var j = i + 1; j < darts.Length; ++j) {
var x1 = darts[i][0];
var y1 = darts[i][1];
var x2 = darts[j][0];
var y2 = darts[j][1];
var x = x2 - x1;
var y = y2 - y1;
if (sign(x * x + y * y - 4 * r * r) > 0) {
continue;
}
var mx = (x1 + x2) / 2.0;
var my = (y1 + y2) / 2.0;
var d = Math.Sqrt(x * x + y * y);
var h = Math.Sqrt(r * r - d * d / 4);
var sin = (y2 - y1) / d;
var cos = (x2 - x1) / d;
var c1 = new double[] {
mx - h * sin,
my + h * cos
};
var c2 = new double[] {
mx + h * sin,
my - h * cos
};
res = Math.Max(res, count(darts, c1, r));
res = Math.Max(res, count(darts, c2, r));
}
}
return res;
}
private int count(int[][] darts, double[] center, int r) {
var res = 0;
for (var i = 0; i < darts.Length; ++i) {
var x = darts[i][0] - center[0];
var y = darts[i][1] - center[1];
if (sign(r * r - x * x - y * y) >= 0) {
res = res + 1;
}
}
return res;
}
private static int sign(double x) {
if (x + 1e-9 < 0)
return -1;
if (x - 1e-9 > 0)
return +1;
return 0;
}
}And this solution is truly deterministic O(n^3) and is about 20 times faster than the first approach and consumes 3 times less memory:
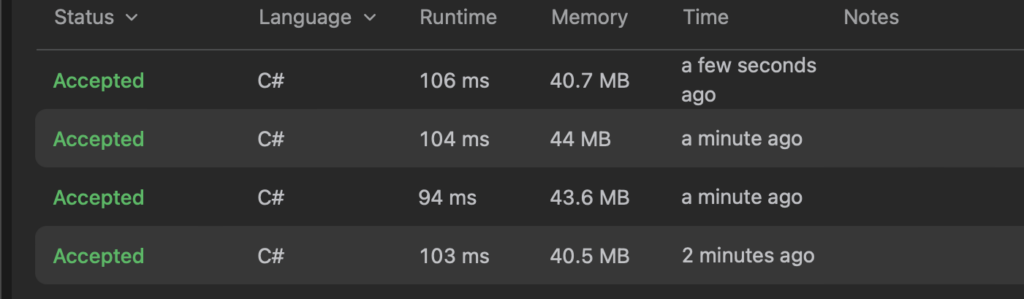
Bonus: the sweep line
Initially We started discussing this problem as an example of the sweep line technique. So, there is yet another elegant solution that is based on this method, which I also learned today from my colleague:
- Start from a point A in the dataset and draw any circle of radius R that passes through A.
- Begin rotating this circle around A while keeping track of events where the circle intersects with other points in the dataset. Save these events as pairs (angle, sign), where the sign is +1 if a new point is encountered and -1 if a point is discarded.
- Sort all the events for a given point by angle. Then, calculate the sum of signs and update the results accordingly.
Since, for a given point, we check and sort at most n events, the total time complexity is O(n^2 log(n)), which is quite impressive.
The implementation for this method was also shared with me:
public class Solution {
public int NumPoints(int[][] darts, int r)
{
if (darts.Length < 2)
{
return darts.Length;
}
return new Large().Solve(darts, r);
}
private class Large {
public int Solve(int[][] darts, int r) {
var res = 1;
for (var i = 0; i < darts.Length; ++i) {
var x1 = darts[i][0];
var y1 = darts[i][1];
var ang = new List<(double, int)>();
for (var j = 0; j < darts.Length; ++j) {
if (i == j) {
continue;
}
var x2 = darts[j][0];
var y2 = darts[j][1];
var x = x2 - x1;
var y = y2 - y1;
var d = Math.Sqrt(x * x + y * y);
if (sign(d - 2 * r) > 0) {
continue;
}
var rot = Math.Atan2(y, x);
var phi = Math.Acos(d / r * 0.5);
ang.Add((rot - phi, +1));
ang.Add((rot + phi, -1));
}
ang.Sort((a, b) => {
if (a.Item1.CompareTo(b.Item1) != 0) {
return a.Item1.CompareTo(b.Item1);
} else {
return b.Item2.CompareTo(a.Item2);
}
});
var cnt = 1;
for (var j = 0; j < ang.Count; ++j) {
cnt += ang[j].Item2;
if (res < cnt) {
res = cnt;
}
}
}
return res;
}
}
private static int sign(double x) {
if (x + 1e-9 < 0)
return -1;
if (x - 1e-9 > 0)
return +1;
return 0;
}
}Conclusions
To be honest I find this problem challenging and quite intricate. Solving it individually within 30-60 minutes, especially if encountering it for the first time, is quite a feat. But I am grateful to have colleagues with whom I can collaboratively learn how to tackle such complex problems during coffee breaks.